电路概述⚓︎

约 1898 个字 1 张图片预计阅读时间 6 分钟

graph LR
A(电路)==>B(集中参数电路)
A-->C(分布参数电路)
B==>D(线性电路)
B==>E(非线性电路)
D==>F(稳态电路)
D==>G(暂态电路)
F==>H(直流稳态)
F==>I(正弦交流稳态)
F==>J(非正弦交流稳态)
F-->K(复杂电路稳态)
G==>L(时域分析方法)
G-->M(频域分析方法)

电路模型⚓︎

电路

电路是由若干电气设备或元器件按一定方式组合起来的整体。
电路的作用是传输、存储电能或变换、处理电信号。
电路原理的研究对象是由实际电路抽象而成的理想化的电路模型。
这种抽象化的基本物理模型就称为理想电路元件。
实际电路元件是理想电路元件的组合。
在不同的运行条件下，一个实际电路可简化为不同的电路模型。

电路元件

graph LR
Z(电路元件)==>A(负载)
Z==>B(电源)
A==>C(电阻元件)
A==>D(电感元件)
A==>E(电容元件)
B==>F(独立电源元件)
B==>G(受控源元件)

电路元件⚓︎

电阻⚓︎

电阻元件是体现电能转化为其它形式能量的二端元件，简称电阻Resistor。电阻的端电压与电流有确定的函数关系，用字母R表示，符号为\(\Omega\)。

凡是端电压与端电流成正比的电阻元件称为线性电阻，否则称为非线性电阻。

电导⚓︎

\[ G = \frac{1}{R} \]

称为电导，用字母G表示，单位为西门子S。

电阻元件消耗功率和消耗热量的关系为

\[ P=UI\\ W=\int_0^t p \mathrm{d}t \]

若电阻元件为线性电阻，则可以表示为

\[ P = I^2 R = \frac{U^2}{R}\\ W = Pt = I^2 Rt \]

作用

用途：阻碍电流通过
作用：分流、限流、分压、降压、滤波（与电容器组合使用）和阻抗匹配等。

电容⚓︎

电容元件Capacitor是体现电场能量的二端元件，用字母C表示，单位为法拉F，常用的有\(\mu F\)、\(pF\)。

线性电容⚓︎

线性电容上储存的电荷\(q\)与端电压\(u_C\)之间的关系

\[ q=Cu_C \]

当电流与线性电容电容电压方向相同时，电流与电容的关系为

\[ i_C=\frac{\mathrm{d}q}{\mathrm{d}t}=C\frac{\mathrm{d}u_C}{\mathrm{d}t} \]

线性电容电容电压具有“记忆”功能

\[ u_C(t)=u_C(t_0)+\frac{1}{C}\int_{t_0}^t i_C(\xi)\mathrm{d}\xi \]

电容

电容对直流具有隔离作用（相当于开路）
电容器是一种储能原件，具有“隔直通交阻低频”的特性

电容的作用

降压限流电容
移相电容
定时（延时）电容
滤波电容
旁路电容
耦合电容

电感⚓︎

电感元件inductor是体现磁场能量的二端元件，用字母\(L\)表示，其单位为亨利（\(H\)），常用的有\(mH\)、\(\mu H\)。

电感交链的磁通链\(\varphi\)与电流\(i\)的关系为

\[ \varphi = Li\\ \varphi = W\phi \]

线性非时变电感的电压与电流关系为

\[ u_L=\frac{\mathrm{d}\varphi}{\mathrm{d}t}=L\frac{\mathrm{d}i_L}{\mathrm{d}t} \]

注意

对于直流电来说，电感元件相当于一根短接导线。

电感的作用

电感的作用：通直流，阻交流

移压限流
移相
定时（延时）
扼流
滤波
震荡

电源⚓︎

电源是将其他形式的能转化为电能的设备。

电源形式

交流电AC Alternating Current

直流电DC Direct Current

相互转化

简称	全称
`AC-DC`	整流器
`DC-AC`	逆变器
`AC-AC`	矩阵变换器
`AC-DC-AC`	变频器
`DC-DC`	开关电源

电源也常称为激励、信号或输入。在激励作用下，电路某处出现的电压和电流，就称为响应或输出。

独立源⚓︎

独立源的量值不随电路中其它物理量的改变而改变。

当电源以恒定电压的方式输出时，称为理想电压源。

理想电压源

一个实际电压源可以用一个理想电压源和内电阻\(R_0\)相串联的电路模型来表示。

\[ U=E-R_0 I \]

实际电压源内阻越小，就越接近理想电压源。

注意

非零电压源不能直接短路，两个不等值的电压源不能并联。

当电源以恒定电流的方式输出时，称为理想电流源。

理想电流源

一个实际电流源可以用一个理想电流源和内阻\(R_S\)相并联的电路模型来表示。

\[ I = I_S - \frac{U}{R_S} \]

实际电流源的内阻越大，越接近理想电流源。

注意

非零电流源不能开路，两个不等值的电流源不能串联。

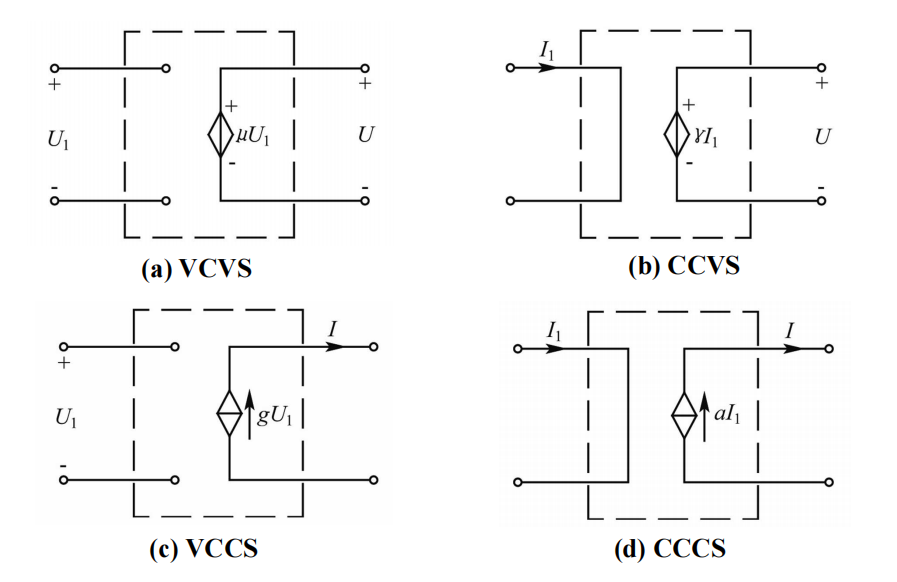
受控源⚓︎

受控源又有受控电压源和受控电流源之分。按其控制量的不同，共有4种表示形式。

受控源

那么，如何分辨受控源的控制量和源类型呢？

控制量：由控制系数后面的字母来判断。若为\(U\)，则控制量为电压；若为\(I\)，则控制量为电流。

源类型：

可以直接由图标判断（推荐），若图标为电流源即为电流源，图标为电压源则为电压源
可以由公式量纲判断（不推荐），如\(\mu U\)为电压控制电压源，\(gU\)则为电压控制电流源

\[ 受控源 \begin{cases} U=\mu U_1 &\text{电压控制电压源(VCVS)}\\ U=\gamma I_1 &\text{电流控制电压源(CCVS)}\\ I=gU_1 &\text{电压控制电流源(VCCS)}\\ I=\alpha I_1 &\text{电流控制电流源(CCCS)} \end{cases} \]

控制系数

r——转移电阻，具有电阻的量纲\(\Omega\)

g——转移电导，具有电导的量纲S

\(\mu\)、\(\alpha\)分别为电压放大倍数和电流放大倍数，无量纲

控制系数为常数时的受控源称为线性受控源。

参考方向⚓︎

电流参考方向

电流方向是客观存在的，但在分析复杂电路时，往往事先难以判断某支路中电流的实际方向。为此，在分析和计算电路时，常可选定某一方向作为电流的正方向，称为参考方向。

说明

电流的参考方向可以任意选取，但一旦选定之后，在分析过程中就不能再改变。
电流实际方向与参考方向一致时，电流取正值，反之取负。

电压参考方向

用由正极指向负极的方向为电压的参考方向。

注意

电压的参考方向为电势的下降方向，不是升高方向！

关联参考方向⚓︎

当元件的电压和电流的参考方向一致时，即电流从电压正端流向负端时 (1) ，称为电压电流的关联参考方向。

可以这样想：正电荷从高电势流向低电势，能量下降

\[ P=UI \begin{cases} >0 &\text{元件实际消耗功率}\\ <0 &\text{元件实际输出功率} \end{cases} \]

若元件的电压电流为非关联参考方向，则正好相反。

基尔霍夫定律⚓︎

基本概念

概念	解释
支路	单个或若干个二端元件串联成的电路
节点	两条以上支路的交汇点
回路	若干条支路组成的闭合路径
网孔	内部不包含支路的回路
支路电流	每条支路上流过的电流
支路电压	每条支路两端的电压

基尔霍夫电流定律⚓︎

基尔霍夫电流定律KCL：电路中任一节点的代数和为零

\[ \sum i=0 \]

其中，流出节点的电流与流入节点的电流正负号相反。

推论

在任一瞬时，流入某个节点的电流之和等于流出节点的电流之和。即

\[ \sum I_{出}=\sum I_{入} \]

提示

中学学到的“干路电流是所有支路电流之和”，其实是基尔霍夫电流定律的特殊情况，相当于取的分叉节点。
根据基尔霍夫电流定律可知，对于任意一个电路元件（如电源），其输出电流一定等于输入电流。这句话看起来显而易见，在实际电路分析中却可能被遗忘。

广义KCL⚓︎

基尔霍夫电流定律不仅适用于节点，也可以推广应用于电路中的某一部分。

流进任一闭合面的电流的代数和为零。

——广义的KCL

基尔霍夫电压定律⚓︎

基尔霍夫电压定律KVL：在任一瞬时，电路任一闭合回路中各支路电压的代数和为零。

\[ \sum u = 0 \]

支路电压方向与回路绕行方向一致时取正号，反之取负号。

推论

KVL的另一个形式为

\[ \sum RI=\sum U_S \]

任一支路电阻压降代数和等于电压源压升代数和。

提示

中学学到的“并联电路各支路电压相等”，其实是基尔霍夫电压定律的特殊情况。两个并联支路之间没有电阻，必定会有\(U_1 + (-U_2) = 0\)。

注意

更本质地来说，其实KVL只是在阐述一个事实：电压的本质是电势差，而每个节点的电势只有一个。

因此，只要在电路中满足了这个条件，列出的方程就会自动满足KVL。